Código
options(OutDec = ",", digits = 4)
library(dplyr)
library(survival)
library(ggplot2)options(OutDec = ",", digits = 4)
library(dplyr)
library(survival)
library(ggplot2)Na análise de sobrevivência, métodos não paramétricos estimam funções sem assumir uma distribuição prévia para o tempo de falha. O estimador de Kaplan-Meier, por exemplo, calcula probabilidades diretamente dos dados, sendo útil para comparar curvas de sobrevivência entre grupos. No entanto, essa abordagem não permite avaliar diretamente o impacto de covariáveis, como idade ou tipo de tratamento, sobre a sobrevivência.
Os modelos paramétricos, por outro lado, assumem uma distribuição específica para o tempo de ocorrência do evento, permitindo estimativas mais estruturadas e eficientes. Assim como ocorre em modelos de regressão (linear, Poisson, logístico), esses métodos possibilitam relacionar covariáveis diretamente ao tempo de sobrevivência, garantindo uma análise mais detalhada e interpretável.
Entretanto, quais distribuições de probabilidade são adequadas para representar o tempo até a ocorrência do evento de interesse? Como o tempo de sobrevivência \(T\) é uma variável contínua e não negativa, algumas distribuições comuns — como a normal — não são apropriadas, pois permitem valores negativos. Além disso, dados de sobrevivência frequentemente apresentam assimetria à direita, indicando que poucos indivíduos sobrevivem por períodos longos enquanto a maioria tem eventos precoces. Reforçando a inadequação de algumas distribuições para representação probabilística do tempo de sobrevivência.
Se \(T \sim \text{Exponencial}(\alpha)\). Sua função densidade de probabilidade é expressa da seguinte forma:
\[ f(t) = \alpha \exp\left\{ -\alpha t \right\}. \tag{3.1}\]
Desta forma, podemos obter a função sobrevivência com base no completar da distribuição acumulada de \(T\):
\[\begin{align*} S(t) & = P(T > t) = 1 - P(T \leq t) = 1 - F(t) \\ & = 1 - \left[1 - \exp\left\{ -\alpha t \right\}\right]. \end{align*}\]Assim definimos, formalmente, a função sobrevivência como:
\[ S(t) = \exp\left\{ -\alpha t \right\}. \tag{3.2}\]
Note que o parâmetro \(\alpha\) é a velocidade de queda da função sobrevivência. Através das relações entre as funções em análise de sobrevivência, temos a função risco ou taxa de falha. Obtida pela razão entre da função densidade de probabilidade e a função sobrevivência:
\[ \lambda(t) = \dfrac{f(t)}{S(t)} = \dfrac{\alpha \exp\{ -\alpha t \}}{\exp\{ -\alpha t \}} = \alpha. \tag{3.3}\]
Sendo a função risco constante para todo tempo observado \(t\), o risco acumulado é função linear no tempo com inclinação da reta dada por \(\alpha\):
\[ \Lambda(t) = - \ln\left\{S(t)\right\} = - \ln\left\{ \exp\{ -\alpha t \} \right\} = - (- \alpha t) = \alpha t \tag{3.4}\]
Veja, a seguir, a Figura 3.1 que mostra as curvas de densidade de probabilidade, de sobrevivência, risco e risco acumulado para diferentes valores do parâmetro \(\alpha\).
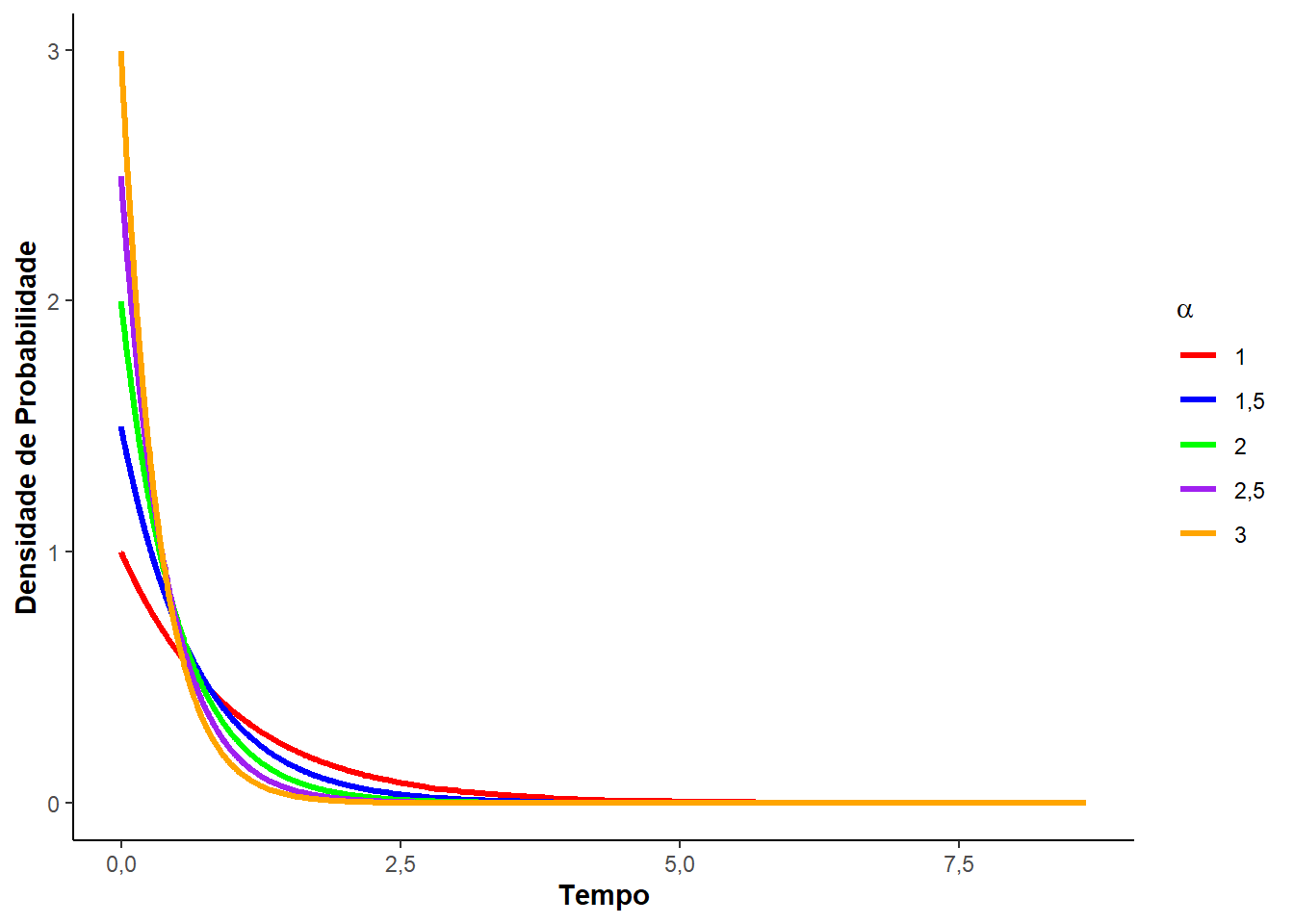
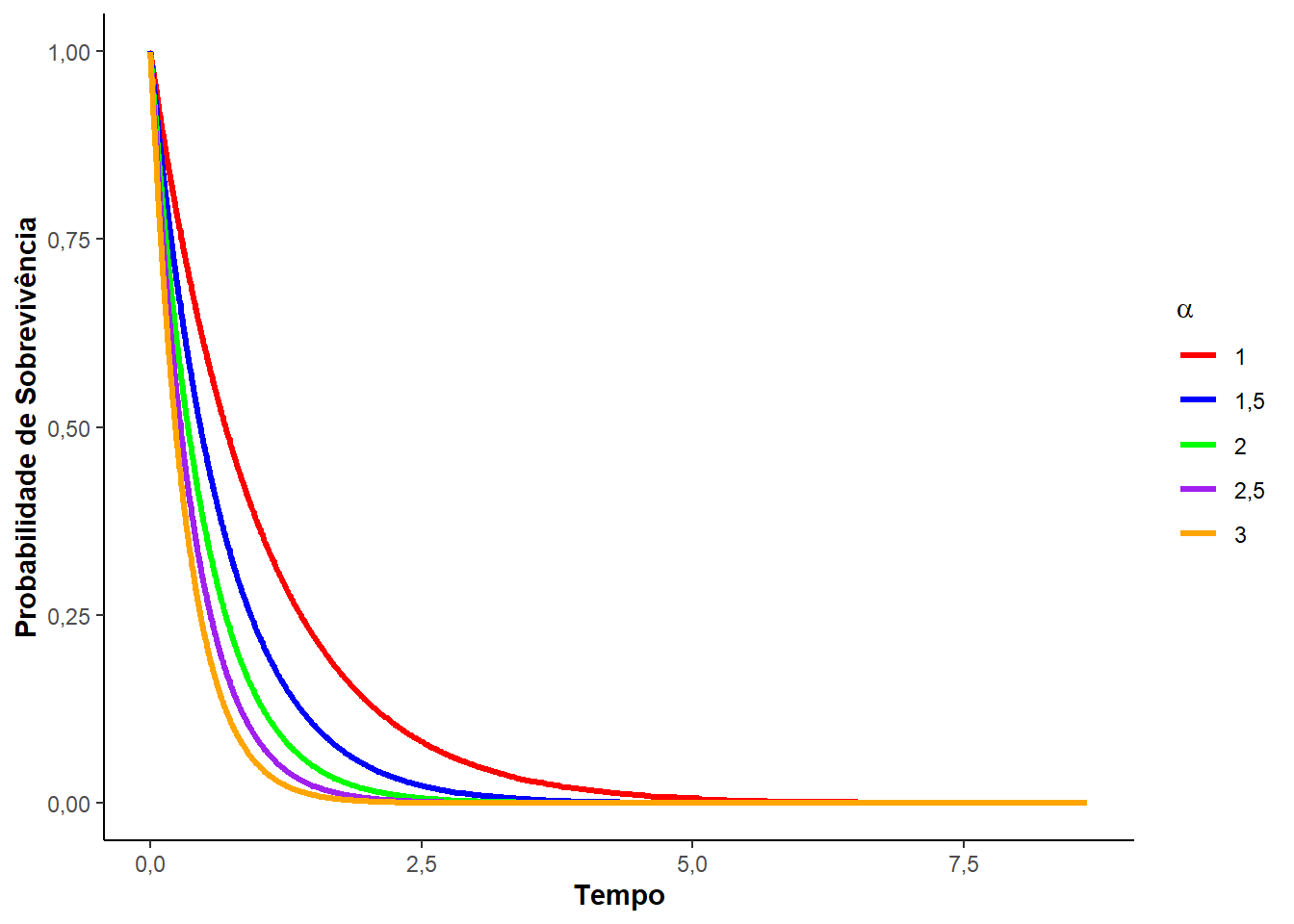
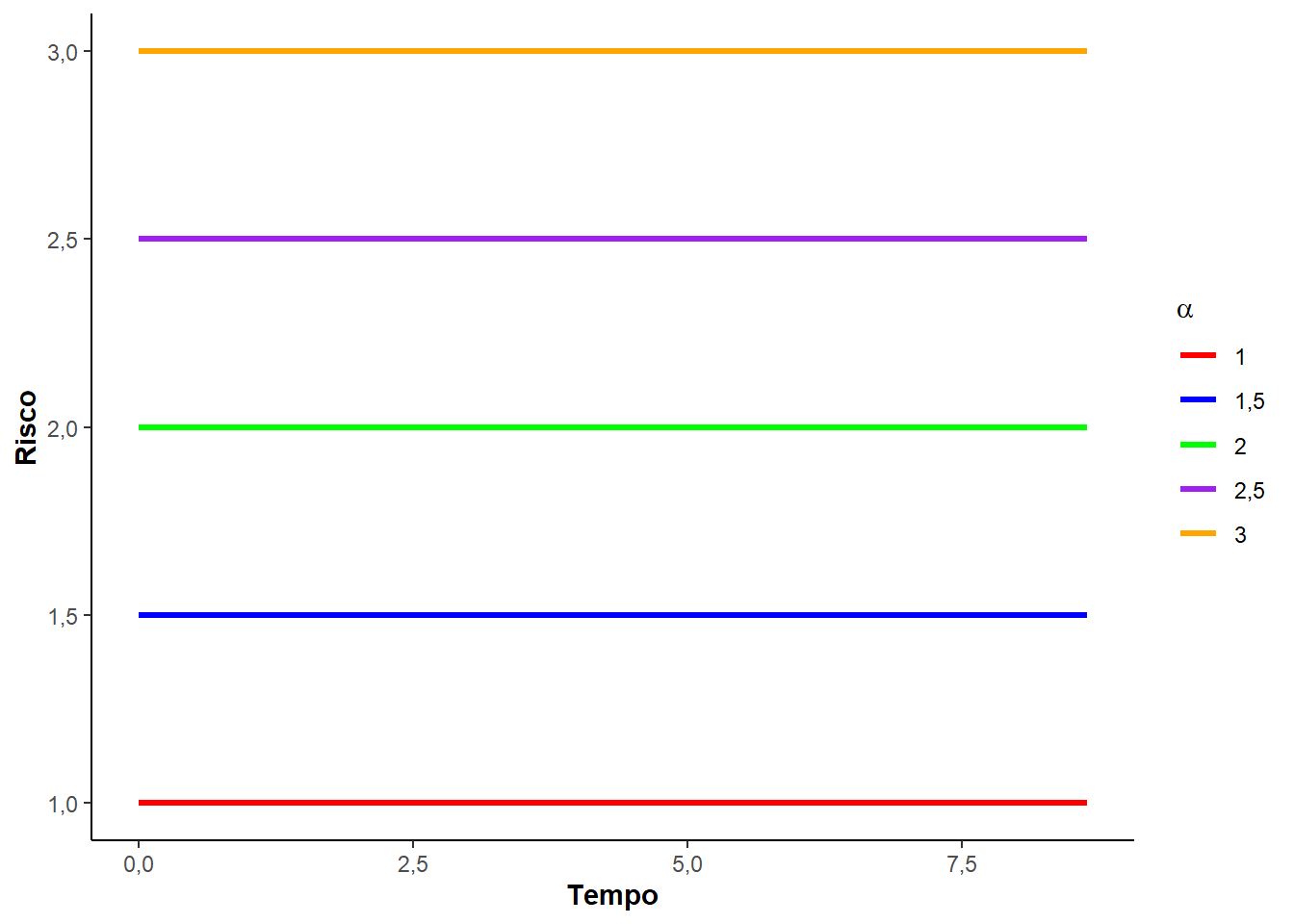

Note que, o parâmetro \(\alpha\) deve ser sempre positivo e quanto maior o valor de \(\alpha\) (taxa), mais abruptamente a função sobrevivência \(S(t)\) decresce, e maior é a inclinação da função de risco acumulado. Quando \(\alpha = 1\), a distribuição é denominada exponencial padrão.
A distribuição exponencial, por possuir um único parâmetro, é matematicamente simples e apresenta um formato assimétrico. Seu uso em análise de sobrevivência tem uma analogia com a suposição de normalidade em outras técnicas e áreas da estatística. Entretanto, a suposição de risco constante associada a essa distribuição é bastante restritiva e, em muitos casos, pode não ser realista. Essa característica da distribuição exponencial é conhecida como falta de memória, o que significa que o risco futuro é independente do tempo já decorrido.
A média e a variância do tempo de sobrevivência, para uma variável que segue a distribuição exponencial, são expressas como funções inversas do parâmetro de taxa (\(\alpha\)). Assim, quanto maior o risco, menor o tempo médio de sobrevivência e menor a variabilidade em torno da média. As expressões são dadas por:
\[ E\left[T\right] = \dfrac{1}{\alpha}, \]
\[ Var\left[T\right] = \dfrac{1}{\alpha^2}. \]
Como a distribuição de \(T\) é assimétrica, se torna mais usual utilizar o tempo mediano de sobrevivência ao invés de tempo médio. Pode-se obter o tempo mediano de sobrevivência a partir de um tempo \(t\), tal que, \(S(t) = 0,5\), logo,
\[\begin{align*} S(t) & = 0,5 \Leftrightarrow \exp\left\{ -\alpha t \right\} = 0,5 \Leftrightarrow -\alpha t = \ln\left\{2^{-1}\right\} \\ \alpha t & = - (-\ln\left\{2\right\}) \Leftrightarrow \alpha t = \ln\left\{2\right\}. \end{align*}\]Desta forma, o tempo mediano de sobrevivência é definido como:
\[ T_{mediano} = \dfrac{\ln\left\{2\right\}}{\alpha}. \]
Em resumo, o modelo exponencial é apropriado para situações em que o período do experimento é curto o suficiente para que a suposição de risco constante seja plausível.
Na maioria dos casos de análise de sobrevivência - principalmente na área da saúde - é mais razoável supor que o risco varia ao longo do tempo, em vez de permanecer constante. Atualmente, a Distribuição Weibull é amplamente utilizada, pois permite modelar essa variação do risco ao longo do tempo. Como será demonstrado, a distribuição exponencial é um caso particular da distribuição Weibull.
Se o tempo de sobrevivência \(T\) segue uma distribuição Weibull, isto é, \(T \sim \text{Weibull}(\gamma, \alpha)\), sua função densidade de probabilidade é dada por:
\[ f(t) = \dfrac{ \gamma }{ \alpha^{\gamma} } t^{\gamma - 1} \exp \left\{ - \left( \dfrac{t}{\alpha} \right)^{\gamma} \right\}. \tag{3.5}\]
A partir da Equação 3.5 é possível chegar a função sobrevivência da distribuição Weibull sendo está função definida como:
\[ S(t) = \exp \left\{ - \left( \dfrac{t}{\alpha} \right)^{\gamma} \right\}, \tag{3.6}\]
A função risco, \(\lambda(t)\), depende do tempo de sobrevivência. Apresentando variação no tempo conforme a expressão:
\[ \lambda (t) = \dfrac{f(t)}{S(t)} = \dfrac{ \gamma }{ \alpha^{\gamma} } t^{\gamma - 1} \tag{3.7}\]
e a função risco acumulado da distribuição Weibull é dada por:
\[ \Lambda (t) = - \ln\left\{S(t)\right\} = - \ln \left\{ \exp \left\{ - \left( \dfrac{t}{\alpha} \right)^{\gamma} \right\} \right\} = \left( \dfrac{t}{\alpha} \right)^{\gamma}. \tag{3.8}\]
Note que, o parâmetro \(\gamma\) determina a forma função risco da seguinte maneira:
Veja, a seguir, a Figura 3.2 que mostra as curvas de densidade, sobrevivência, risco e risco acumulado para diferentes valores do parâmetro de forma \(\gamma\) e o de escala \(\alpha = 1\).
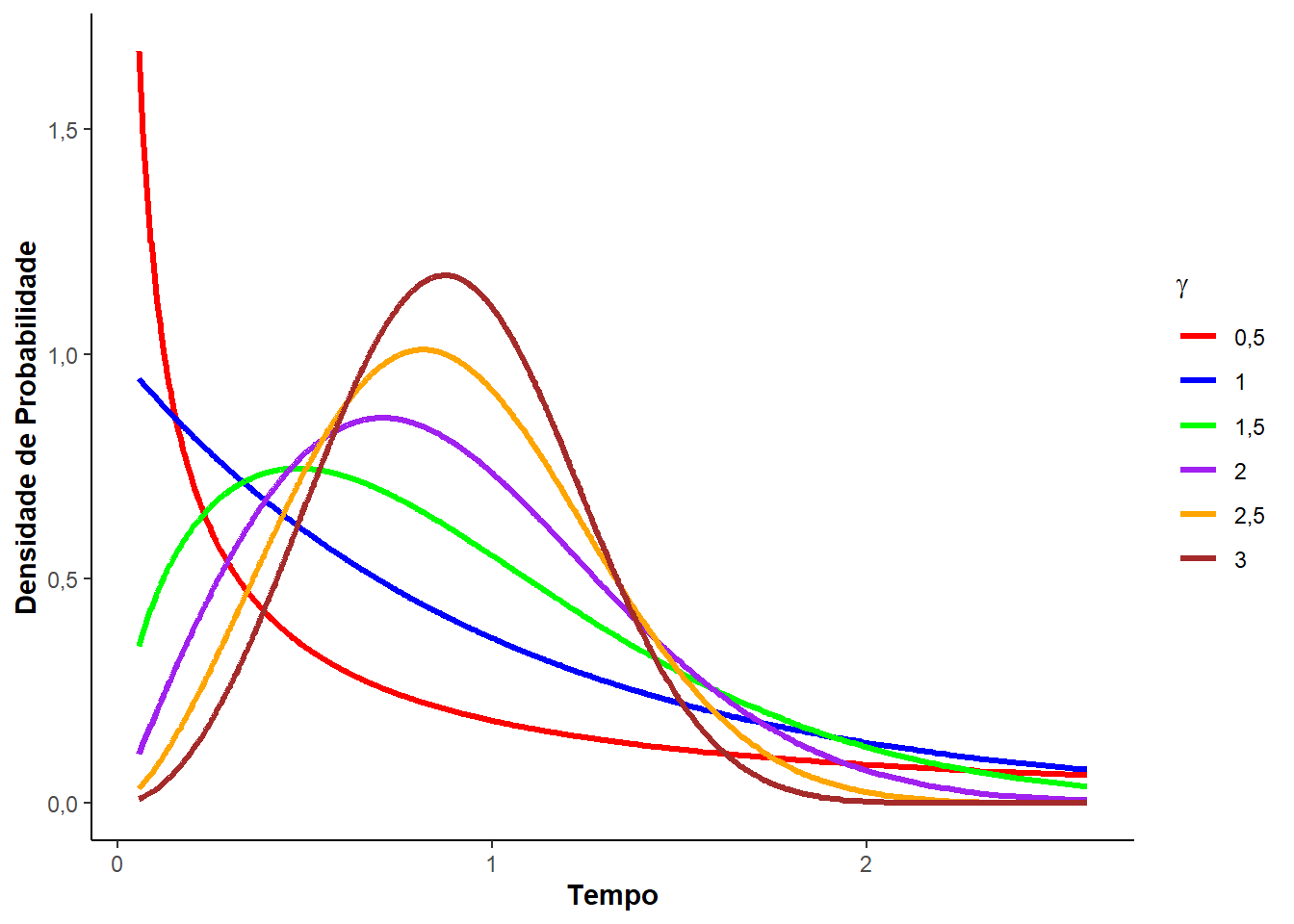
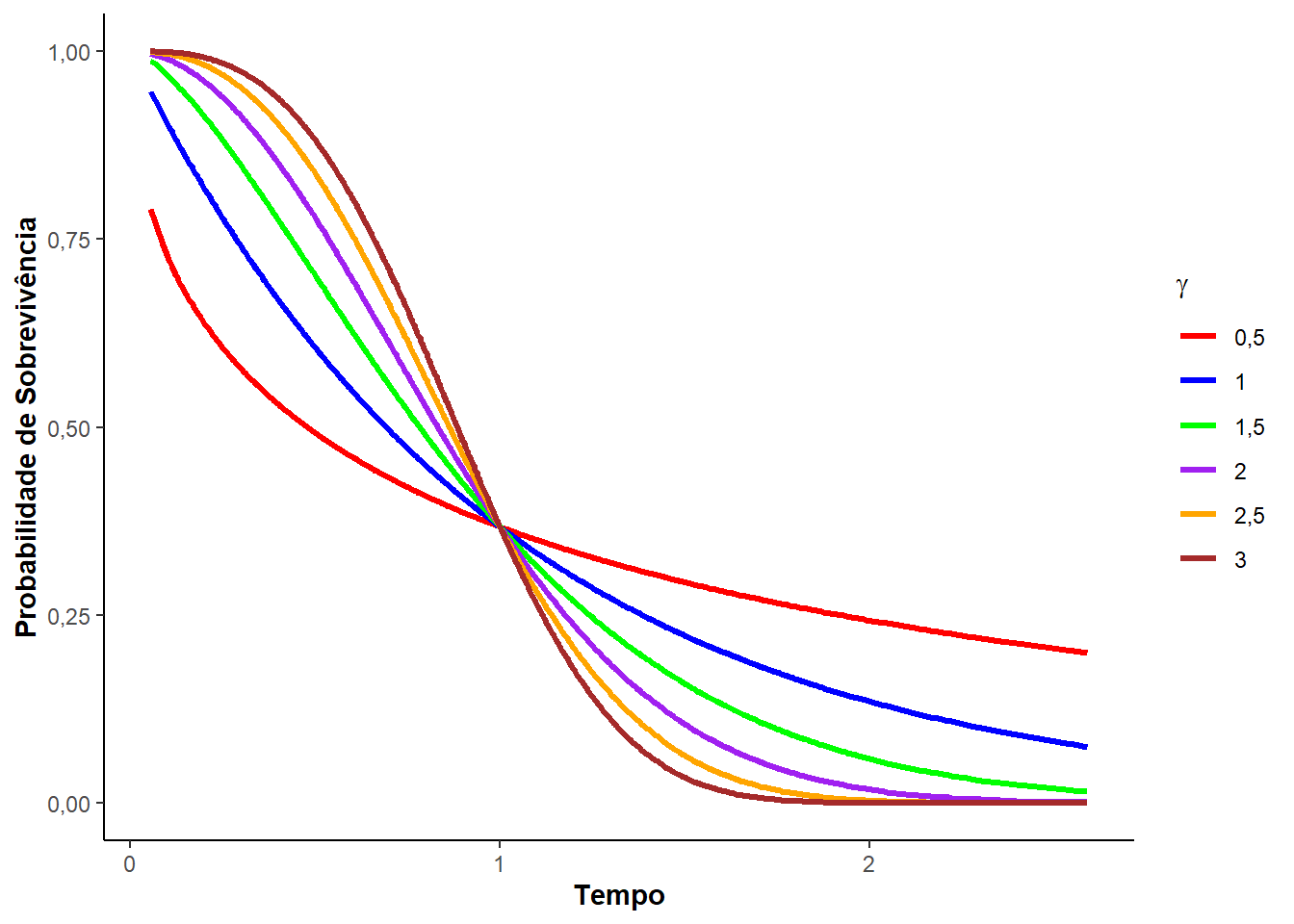
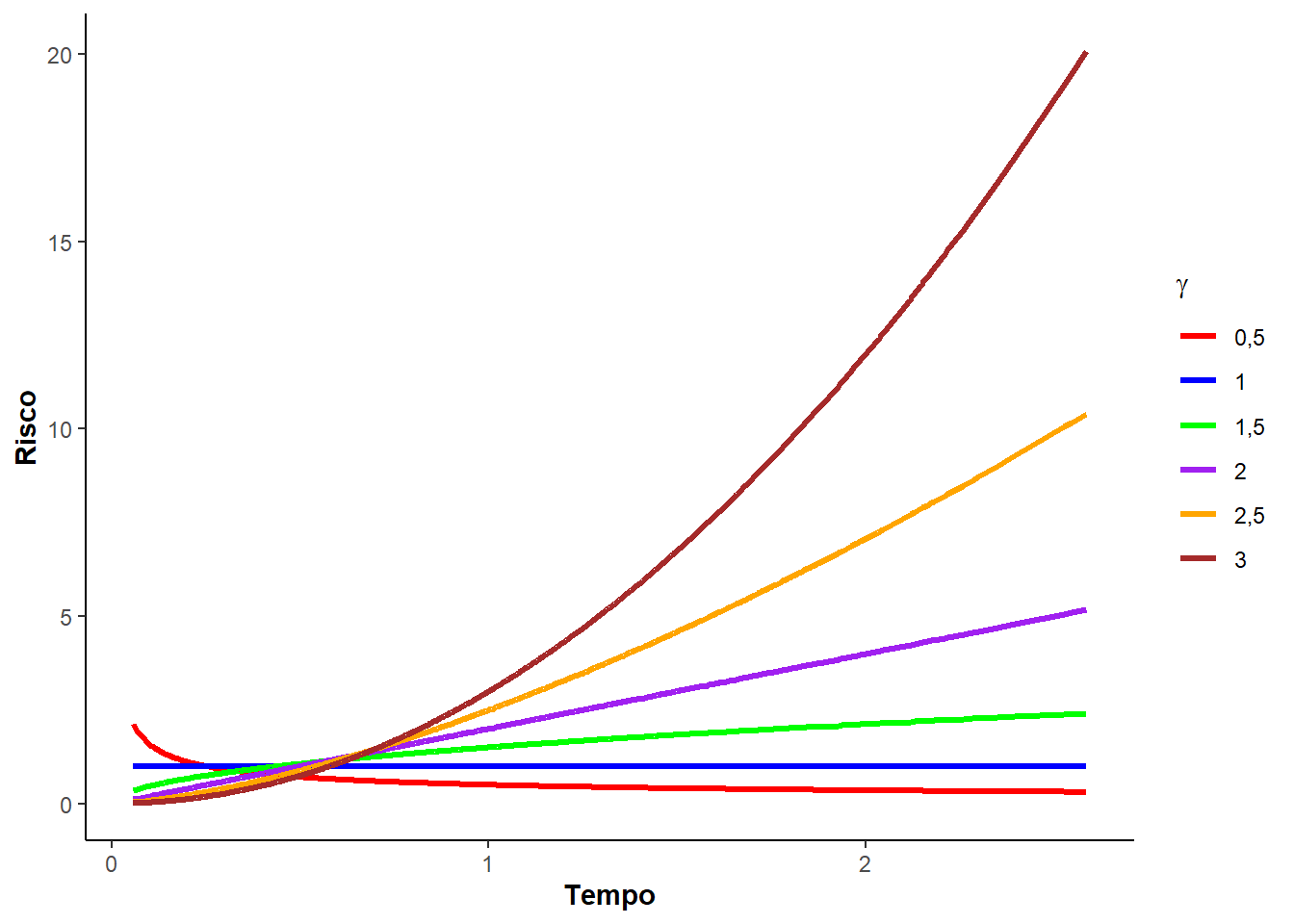
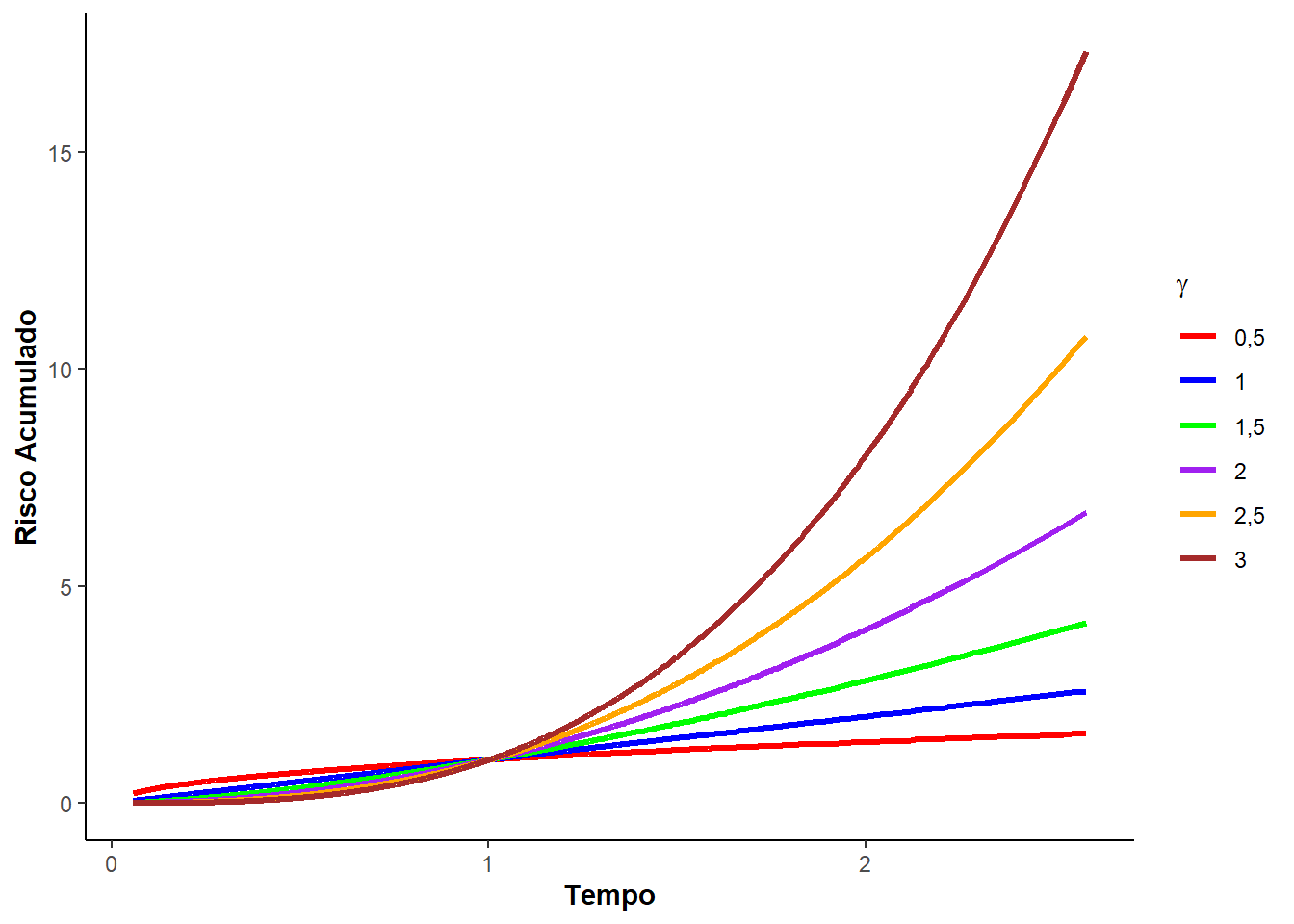
Perceba que \(\alpha\) - parâmetro escala - e \(\gamma\) - parâmetro de forma - são definidos dentro dos \(\mathbb{R}^{+}\). É incluso a função Gama na média e variância da distribuição Weibull, assim,
\[ E[T] = \alpha \Gamma\left[1 + (1/\gamma)\right] \] e
\[ Var[T] = \alpha^{2} \left[ \Gamma \left[1 + (2/\gamma)\right] - \Gamma\left[1 + (1/\gamma)\right]^{2} \right] \]
sendo a função Gama \(\Gamma [k]\) expressa por \(\Gamma [k] = \int_{0}^{\infty} t^{k -1} \exp\{t\} dt\). Afim de se obter o tempo mediano de sobrevivência, igualamos a probabilidade de sobrevivência a \(0,5\). Desta forma:
\[\begin{align*} S(t) & = 0,5 \Leftrightarrow \exp \left\{ - \left( \dfrac{t}{\alpha} \right)^{\gamma} \right\} = 0,5 \\ - \left( \dfrac{t}{\alpha} \right)^{\gamma} & = \ln\left\{2^{-1}\right\} \Leftrightarrow \left( \dfrac{t}{\alpha} \right)^{\gamma} = \ln\left\{2\right\} \\ \dfrac{t}{\alpha} & = \left[ \ln\left\{2\right\} \right]^{1/\gamma}. \end{align*}\]Logo, definimos o tempo mediano de sobrevivência da distribuição Weibull como:
\[ T_{mediano} = \alpha [\ln{(2)}]^{1/\gamma}. \]
Uma alternativa para modelar o tempo de sobrevivência é a distribuição log-normal. Dizemos que uma variável aleatória \(T\) tem distribuição log-normal com parâmetros \(\mu\) e \(\sigma^{2}\), denotado por \(T \sim \text{Log-normal}(\mu, \sigma^2)\), quando o logaritmo natural de \(T\), ou seja, \(T^{*} = \ln\left\{T\right\}\), segue uma distribuição normal, isto é, \(T^{*} \sim \text{Normal}(\mu, \sigma^2)\). Nesse caso, \(\mu\) e \(\sigma^2\) correspondem à média e variância de \(\ln\left\{T\right\}\). De forma equivalente, pode-se dizer que se \(T^{*} \sim \text{Normal}(\mu, \sigma^2)\), então \(T = \exp\left\{T^{*}\right\} \sim \text{Log-normal}(\mu, \sigma^2)\). A função densidade de probabilidade da distribuição log-normal é dada por:
\[ f(t) = \frac{1}{t \sigma \sqrt{2\pi}} \exp\left\{ -\frac{1}{2} \left(\frac{\ln(t) - \mu}{\sigma}\right)^2 \right\}. \tag{3.9}\]
Quando o tempo de sobrevivência segue essa distribuição, a função sobrevivência \(S(t)\) é expressa por meio da função de distribuição da normal padrão:
\[ S(t) = \Phi\left( \frac{-\ln\left\{t\right\} + \mu}{\sigma} \right). \tag{3.10}\]
Já as funções risco e risco acumulado não têm formas analíticas simples. Porém, podem ser obtidas por meio das relações entre as funções de análise de sobrevivência. Com isso, definimos, respectivamente, a função risco e a função risco acumulado pelas expressões:
\[ \lambda(t) = \frac{f(t)}{S(t)}, \quad \Lambda(t) = -\ln\left\{S(t)\right\}. \]
A Figura 3.3 ilustras as curvas usadas na análise de sobrevivência segundo uma distribuição log-normal, variando o parâmetro de locação \(\mu\) e fixando o parâmetro de escala \(\sigma = 1\).
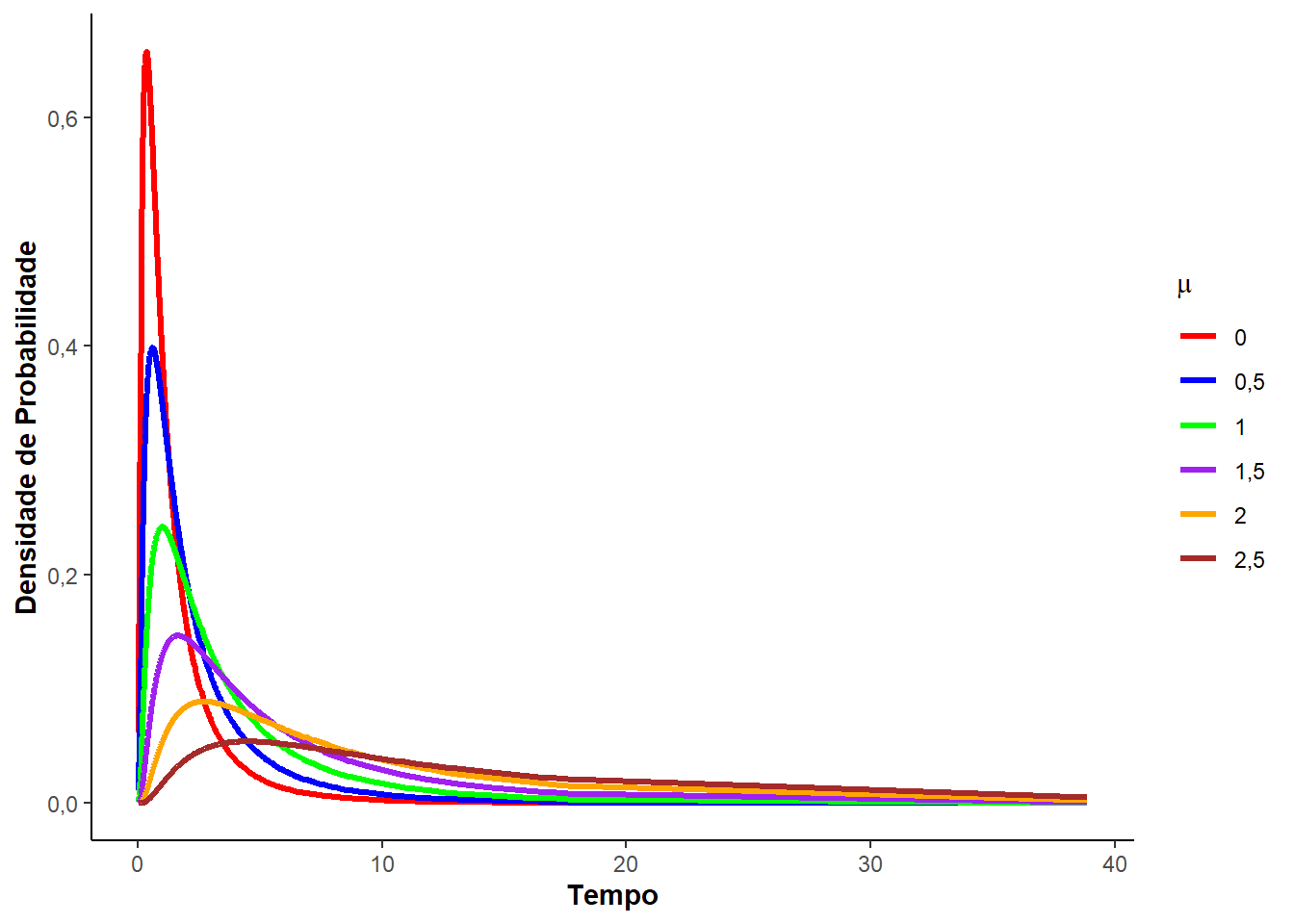


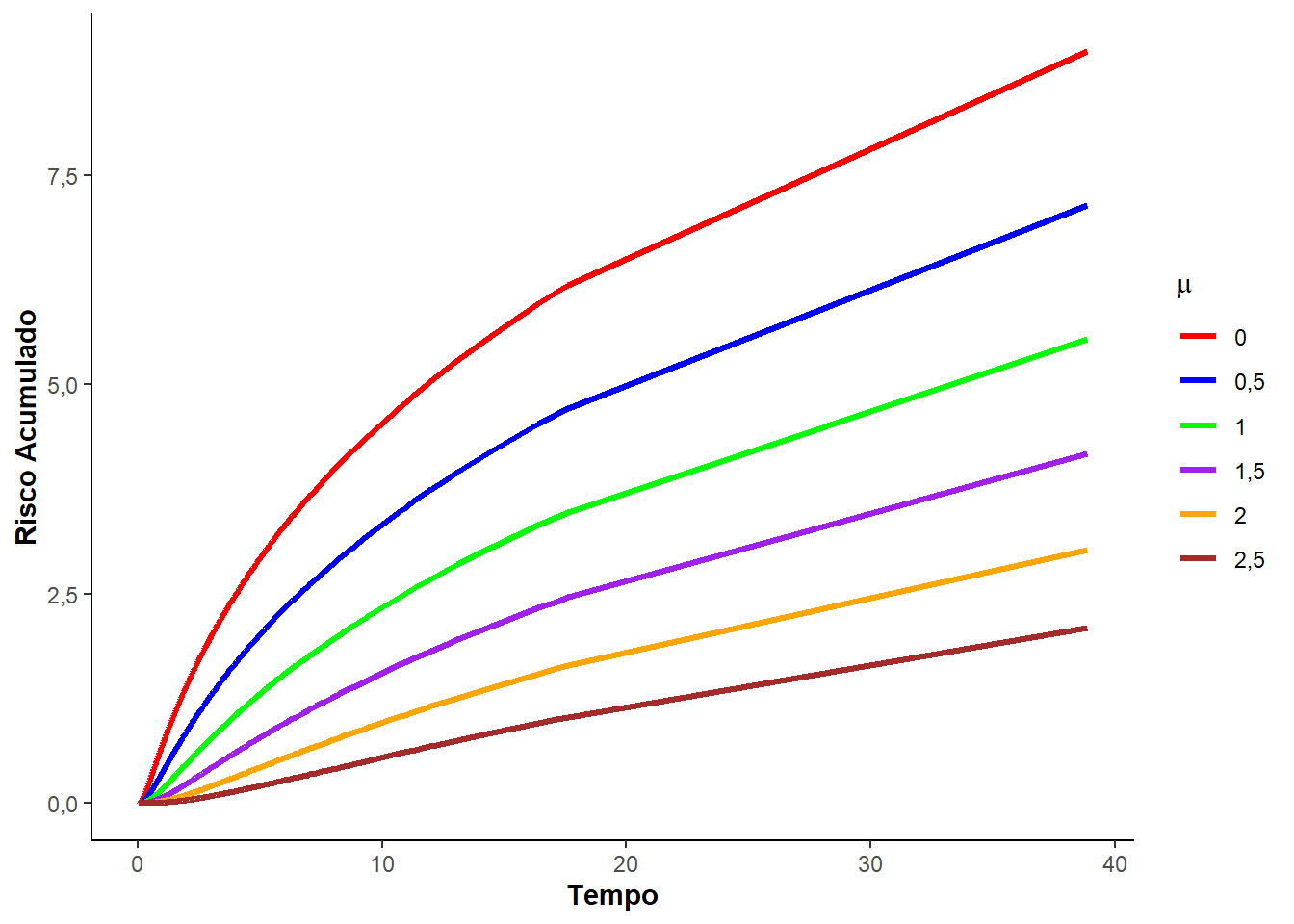
O valor esperado e a variância da distribuição log-normal podem ser expressas em termos da distribuição normal. Desta forma, o valor esperado de \(T\) é expresso por:
\[ E[T] = \exp\left\{\mu + \sigma^{2} / 2\right\}. \]
Já a variância de \(T\) é dada por:
\[ Var[T] = \exp\left\{2 \mu + \sigma^{2} \right\} \cdot (\exp\left\{\sigma^{2}\right\} - 1). \]
Foram apresentados alguns modelos probabilísticos. Esses modelos possuem quantidades desconhecidas, denominadas parâmetros, ou parâmetro, quando o modelo depende de uma única quantidade desconhecida, como no caso da distribuição exponencial.
O Método de Máxima Verossimilhança baseia-se no princípio de que, a partir de uma amostra aleatória, a melhor estimativa para o parâmetro de interesse é aquela que maximiza a probabilidade daquela amostra ter sido observada (Bussab e Morettin 2010), tornando a amostra mais verossímil.
De forma simples, o método de máxima verossimilhança condensa toda a informação contida na amostra, por meio da função de verossimilhança, para encontrar o(s) parâmetro(s) da distribuição que melhor expliquem os dados. Essa abordagem utiliza o produtório das densidades \(f(t)\) para cada observação \(t_i\), \(i = 1, 2, \ldots, n\). Em livros introdutórios de estatística, a função de verossimilhança é definida da seguinte maneira, para um parâmetro ou vetor de parâmetros \(\boldsymbol{\theta}\):
\[ L(\theta) = \prod_{i = 1}^{n} f(t_{i} | \theta). \]
Observe que \(L\) é uma função de \(\theta\), que pode ser um único parâmetro ou um vetor de parâmetros, como ocorre na distribuição log-normal, onde \(\theta = (\mu, \sigma^2)\). No entanto, em análise de sobrevivência, essa definição tradicional de função de verossimilhança é insuficiente, pois os dados frequentemente apresentam censura, o que implica que o tempo de evento pode ser apenas parcialmente observado.
Para lidar com essa característica, utiliza-se a variável indicadora \(\delta_{i}\), apresentada na Seção 1.5, que identifica se o \(i\)-ésimo tempo é um tempo de evento ou de censura. Com base nessa informação, a função de verossimilhança é ajustada da seguinte forma:
Assim, a função de verossimilhança ajustada, que incorpora dados censurados, é expressa como:
\[\begin{align} L(\theta) & = \prod_{i = 1}^{n} \left[ f(t_{i} | \theta) \right]^{\delta_i} \left[ S(t_{i} | \theta) \right]^{1 - \delta_{i}} \nonumber \\ L(\theta) & = \prod_{i = 1}^{n} \left[ \lambda(t_{i} | \theta) \right]^{\delta_i} S(t_{i} | \theta). \label{eq:verossilGeneric} \end{align}\]Para encontrar o valor de \(\theta\) que maximiza \(L(\theta)\), utiliza-se a derivada do logaritmo de base neperiana da verossimilhança igualada a zero:
\[ \frac{\partial \ln [L(\theta)]}{\partial \theta} = 0. \]
A solução dessa equação fornece o valor de \(\theta\) que maximiza \(\ln [L(\theta)]\), e consequentemente, \(L(\theta)\).
Para algumas distribuições, apresentadas na seção anterior, e outras denifidas na literatura, não há forma analítica para as estimativas de máxima verossimilhança. Assim, as estimativas de tais parâmetros depende de métodos numéricos, sendo o Método Iterativo de Newton-Raphson uma abordagem amplamente utilizada.
O Método de Newton-Raphson é um procedimento iterativo eficiente para resolver equações não lineares, muito empregado na estimação de parâmetros de modelos estatísticos. No ajuste de distribuições o método busca maximizar a função de verossimilhança resolvendo o sistema de equações derivado das condições de otimalidade (gradiente nulo). A fórmula iterativa é:
\[ \theta_{n+1} = \theta_{n} - \mathbf{H}^{-1}(\theta_{n}) \nabla \ln[L(\theta_{n})], \tag{3.11}\]
onde:
O método apresenta vantagens convenientes no ajuste de parâmetros de modelos estatísticos. Uma das vantagens é a eficiência do método, que apresenta convergência rápida quando o ponto inicial \(\theta_{0}\) está próximo dos valores reais dos parâmetros. Outra vantagem, é flexibilidade, pois pode ser aplicado a diversos modelos probabilísticos, como o modelo Weibull, que é amplamente utilizada para modelar tempos de vida e dados de sobrevivência.
Entretanto, deve-se, também, atentar-se aos cuidados na aplicação do método. Pois, a convergência do método não é garantida caso o ponto inicial esteja muito distante da solução ou se as condições de regularidade do modelo não forem atendidas. Outro ponto que merece atenção é o cálculo da matriz Hessiana, que pode ser computacionalmente custoso, especialmente em modelos com maior complexidade.
Para um melhor entendimento do Método Iterativo de Newton-Raphson veja o Apêndice (D) do livro Análise de Sobrevivência Aplicada de Colosimo e Giolo (2006).