Código
options(OutDec = ",", digits = 4)
library(dplyr)
library(survival)
library(ggplot2)
url <- "https://docs.ufpr.br/~giolo/asa/dados/leucemia.txt"
dados <- read.table(url, header = TRUE)options(OutDec = ",", digits = 4)
library(dplyr)
library(survival)
library(ggplot2)
url <- "https://docs.ufpr.br/~giolo/asa/dados/leucemia.txt"
dados <- read.table(url, header = TRUE)As técnicas não paramétricas desempenham um importante papel na análise de sobrevivência, pois permitem a estimativa da função de sobrevivência sem a necessidade de pressupor uma distribuição específica dos tempos até a ocorrência do evento de interesse. Essa abordagem é especialmente útil em estudos onde a distribuição dos tempos de falha é desconhecida ou onde se deseja evitar suposições rígidas sobre sua forma.
Diferentemente dos métodos paramétricos, que assumem distribuições predefinidas (como Weibull ou exponencial), as técnicas não paramétricas operam apenas com a ordenação dos eventos observados, tornando-se mais flexíveis e robustas e particularmente úteis na presença de dados censurados.
Proposto por Kaplan e Meier (1958). É um estimador não paramétrico utilizado para estimar a função de sobrevivência. Tal estimador também é chamado de de estimador limite-produto. O Estimador de Kaplan-Meier é uma adaptação a \(S\left(t\right)\) empiríca que, na ausência de censura nos dados, é definida como:
\[ \hat{S}\left(t\right) = \dfrac{\text{nº de observações que não falharam até o tempo } t}{\text{nº total de observações no estudo}}. \]
\(\hat{S}\left(t\right)\) é uma função que tem um formato gráfico de escada com degraus nos tempos observados de falha de tamanho \(1/n\), onde \(n\) é o tamanho amostral.
O processo utilizado até se obter a estimativa de Kaplan-Meier é um processo passo a passo, em que o próximo passo depende do anterior. De forma suscetível, para qualquer \(t\), \(S\left(t\right)\) pode ser escrito em termos de probabilidades condicionais. Suponha que existam \(n\) pacientes no estudo e \(k \left(\leq n\right)\) falhas distintas nos tempos \(t_{1} \leq t_{2} \leq \cdots \leq t_{k}\). Considerando \(S\left(t\right)\) uma função discreta com probabilidade maior que zero somente nos tempos de falha \(t_{j}\), \(j = 1, \cdots, k\), tem-se que:
\[ S\left(t_{j}\right) = \left(1 - q_{1}\right) \left(1 - q_{2}\right) \cdots \left(1 - q_{j}\right), \tag{2.1}\]
em que \(q_{j}\) é a probabilidade de um indivíduo morrer no intervalo \(\left[t_{j-1}, t{j}\right)\) sabendo que ele não morreu até \(t_{j-1}\) e considerando \(t_{0} = 0\). Ou seja, pode se escrever \(q_{j}\) como:
\[ q_{j} = P\left(T \in \left[t_{j-1}, t_{j}\right) | T \geq t_{j-1}\right), \tag{2.2}\]
para \(j = 1, \cdots, k\). A expressão geral do estimador de Kaplan-Meier pode ser apresentada após estas considerações preliminares. Considere:
Com isso, pode-se definir o estimador de Kaplan-Meier como:
\[ \hat{S}_{KM}\left(t\right) = \prod_{j \text{ : } t_{j} < t} \left( \dfrac{n_{j} - d_{j}}{n_{j}} \right) = \prod_{j \text{ : } t_{j} < t} \left(1 - \dfrac{d_{j}}{n_{j}} \right) \tag{2.3}\]
De forma intuitiva, por assim dizer, a Equação 2.3 é proveniente da Equação 2.1, sendo está, uma decomposição de \(S\left(t\right)\) em termos \(q_{j}\)’s. Assim, a Equação 2.3 é justificada se os \(q_{j}\)’s forem estimados por \(d_{j}/n_{j}\), expresso em termos de probabilidade na Equação 2.2. No artigo original de 1958, Kaplan e Meier provam que a Equação 2.3 é um Estimador de Máxima Verossimilhança (EMV) para \(S\left(t\right)\). Seguindo certos passos, é possível provar que que \(\hat{S}_{KM}\left(t\right)\) é EMV de \(S\left(t\right)\). Supondo que \(d_{j}\) observações falham no tempo tempo \(t_{j}\), para \(j = 1, \cdots, k\), e \(m_{j}\) observações são censuradas no intervalo \(\left[t_{j}, t_{j+1}\right)\), nos tempos \(t_{j1}, \ldots, t_{jm_{j}}\). A probabilidade de falha no tempo \(t_{j}\) é, então,
\[ S\left(t_{j}\right) - S\left(t_{j}+\right), \]
com \(S\left(t_{j}+\right) = \lim_{\Delta t \to 0+} S\left(t_{j} + \Delta t\right)\), \(j = 1, \cdots, k\). Por outro lado, a contribuição para a função de verossimilhança de um tempo de sobrevivência censurado em \(t_{jl}\) para \(l = 1, \ldots, m_{j}\), é:
\[ P\left(T > t_{jl}\right) = S\left(t_{jl}+\right). \]
A função de verossimilhança pode, então, ser escrita como:
\[ L\left(S\left(\cdot\right)\right) = \prod_{j = 0}^{k} \left\{ \left[ S\left(t_{j}\right) - S\left(t_{j}+\right) \right]^{d_{j}} \prod_{l=1}^{m_{j}} S\left(t_{jl}+\right) \right\} \]
Com isso, é possível provar que \(S\left(t\right)\) que maximiza \(L\left(S\left(\cdot\right)\right)\) é exatamente a expressão dada pela Equação 2.3.
Como um estimador de máxima verossimilhança, o estimador de Kaplan-Meier têm interessantes propriedades. As principais são:
A consistência e normalidade assintótica de \(\hat{S}_{KM}\left(t\right)\) foram provadas sob certas condições de regularidade, por Breslow e Crowley (1974) e Meier (1975).
Para que se possa construir intervalos de confiança e testar hipóteses para \(S\left(t\right)\), se faz necessário ter conhecimento quanto variabilidade e precisão do estimador de Kaplan-Meier. Este estimador, assim como outros, está sujeito a variações que devem ser descritas em termos de estimações intervalares. A expressão da variância assintótica do estimador de Kaplan-Meier é dada pela Equação 2.4.
\[ \widehat{Var}\left[\hat{S}_{KM}\left(t\right)\right] = \left[\hat{S}_{KM}\left(t\right)\right]^{2} \sum_{j \text{ : } t_{j} < t} \dfrac{d_{j}}{n_{j} \left(n_{j} - d_{j}\right)} \tag{2.4}\]
A expressão dada na Equação 2.4, é conhecida como fórmula de Greenwood e pode ser obtida a partir de propriedades do estimador de máxima verossimilhança. Os detalhes da obtenção da Equação 2.4 estão disponíveis em Kalbfleisch e Prentice (1980).
Como \(\hat{S}_{KM}\left(t\right)\), para um \(t\) fixo, tem distribuição assintóticamente Normal. O intervalo de confiança com \(100\left(1 - \alpha\right)\)% de confiança para \(\hat{S}_{KM}\left(t\right)\) é expresso por:
\[ \hat{S}_{KM}\left(t\right) \pm z_{\alpha/2} \sqrt{\widehat{Var}\left[\hat{S}_{KM}\left(t\right)\right]}. \]
Vale salientar que para valores extremos de \(t\), este intervalo de confiança pode apresentar limites que não condizem com a teoria de probabilidades. Para solucionar tal problema, aplica-se uma transformação em \(\hat{S}_{KM}\left(t\right)\) como, por exemplo, \(\hat{U}\left(t\right) = \ln\left\{ - \ln\left\{ \hat{S}_{KM}\left(t\right) \right\} \right\}\). Esta transformação foi sugerida por Kalbfleisch e Prentice (1980), tendo sua variância estimada por:
\[ \widehat{Var}\left[\hat{U}\left(t\right)\right] = \dfrac{ \sum_{j:t_{j}<t} \frac{d_{j}}{n_{j}\left(n_{j}-d_{j}\right)} }{ \left[ \sum_{j:t_{j}<t} \ln\left\{ \frac{n_{j}-d_{j}}{n_{j}}\right\} \right]^{2} } = \dfrac{ \sum_{j:t_{j}<t} \frac{d_{j}}{n_{j}\left(n_{j}-d_{j}\right)} }{ \left[\ln\left\{ \hat{S}_{KM}\left(t\right) \right\}\right]^{2} }. \]
Logo, pode-se aproximar um intervalo com \(100 \left(1 - \alpha\right)\%\) de confiança para \(S\left(t\right)\) desta forma:
\[ \left[ \hat{S}_{KM}\left(t\right) \right]^{ \exp\left\{ \pm z_{\alpha/2} \sqrt{\widehat{Var}\left[\hat{U}\left(t\right)\right]} \right\} }. \]
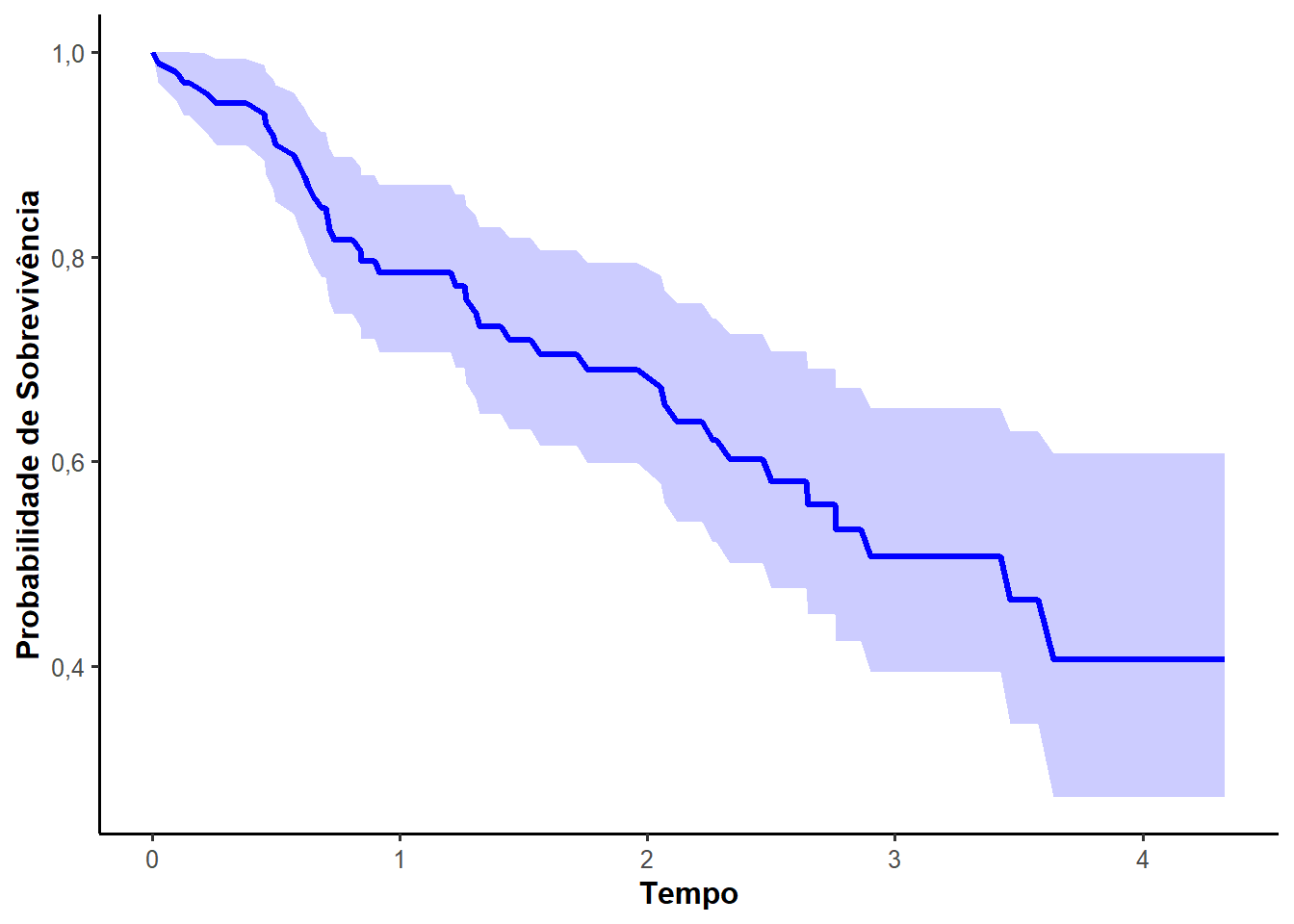
Veja uma aplicação do estimador de Kaplan-Meier para os dados de Leucemia Pediátrica dispostos no Apêndice (A) do livro Análise de Sobrevivência Aplicada de Colosimo e Giolo (2006). De posse do conjunto de dados, pode-se estimar a curva de sobrevivência, tal curva foi ilustrada na Figura 2.1.
# ----------------
# [1] KAPLAN-MEIER
# ----------------
# Estimador de Kaplan-Meier (Pacote survival)
ekm <- survfit(Surv(tempos, cens)~1, data = dados)
# Visualizar Curva de Sobrevivência (Pacote ggplot2)
ggplot(data = NULL, aes(x = ekm$time, y = ekm$surv)) +
geom_line(color = "blue", lwd = 1.2) +
geom_ribbon(aes(ymin = ekm$lower, ymax = ekm$upper), fill = "blue", alpha = 0.2) +
labs(x = "Tempo", y = "Probabilidade de Sobrevivência") +
theme_classic(base_size = 12) +
theme(
axis.title.x = element_text(face = "bold"),
axis.title.y = element_text(face = "bold")
)
O estimador de Kaplan-Meier é amplamente utilizado para estimar a função de sobrevivência \(S(t)\). Ele está disponível em diversos pacotes estatísticos e é frequentemente abordado em materiais introdutórios de estatística. No entanto, dois outros estimadores também possuem relevância na literatura: o estimador de Nelson-Aalen e o estimador de Tabela de Vida.
O estimador de Nelson-Aalen, desenvolvido posteriormente, apresenta similaridades com Kaplan-Meier em termos de propriedades, mas adota uma abordagem diferente ao focar na função risco acumulado \(\Lambda(t)\).
Já o estimador da Tabela de Vida, também chamado de tabela atuarial, tem um importante valor histórico, sendo amplamente utilizado por demógrafos e atuários desde o século XIX sendo empregado principalmente em grandes amostras. Seu uso é especialmente relevante em contextos demográficos e atuariais, como estudos de expectativa de vida e análise de dados censitários.
Nesta seção será abordado apenas o estimador de Nelson-Aalen. Para conhecer mais sobre o estimador da Tabela de Vida ou Tabela Atuarial, consulte a Seção 2.4.2 do livro Análise de Sobrevivência Aplicada de Colosimo e Giolo (2006).
Mais recente que o estimador de Kaplan-Meier, este estimador se baseia na função de sobrevivência expressa da seguinte forma:
\[ S(t) = \exp\left\{ - \Lambda(t) \right\}, \]
em que \(\Lambda(t)\) é a função de risco acumulado apresentada na Seção 1.6.3.
A estimativa para \(\Lambda(t)\) foi inicialmente proposta por Nelson (1972) posteriormente retomada por Aalen (1978) que demonstrou suas propriedades assintóticas utilizando processos de contagem. Na literatura, esse estimador é amplamente conhecido como o estimador de Nelson-Aalen e é definido pela seguinte expressão:
\[ \hat{\Lambda}(t) = \sum_{j:t_{j} < t} \left( \dfrac{d_{j}}{n_{j}} \right), \tag{2.5}\]
onde \(d_{j}\) e \(n_{j}\) são as mesmas definições usadas no estimador de Kaplan-Meier. A variância do estimador, conforme proposta por Aalen (1978), é dada por:
\[ \widehat{Var}\left[\hat{\Lambda}(t)\right] = \sum_{j:t_{j} < t} \left( \dfrac{d_{j}}{n_{j}^{2}} \right). \tag{2.6}\]
Uma alternativa para a estimativa da variância de \(\hat{\Lambda}(t)\), proposta por Klein (1991), é:
\[ \widehat{Var}\left[\hat{\Lambda}(t)\right] = \sum_{j:t_{j} < t} \dfrac{(n_{j} - d_{j})d_{j}}{n_{j}^{3}}, \]
entretanto, o estimador da Equação 2.6 apresenta menor vício, tornando-o mais preferível que o proposto por Klein (1991).
Desta forma, podemos definir, com base no estimador de Nelson-Aalen, um estimador para a função de sobrevivência, podendo ser expressa por:
\[ \hat{S}_{NA}(t) = \exp\left\{- \hat{\Lambda}(t) \right\}. \]
Deve-se, a variância deste estimador, a Aalen e Johansen (1978). Podendo ser mensurada pela expressão:
\[ \widehat{Var}\left[\hat{S}_{NA}(t)\right] = \left[ \hat{S}_{NA}(t) \right]^{2} \sum_{j:t_{j} < t} \left( \dfrac{d_{j}}{n_{j}^{2}} \right). \]
Uma aplicação do estimador de Nelson-Aalen foi desenhada na Figura 2.2 em dois subgráficos. O primeiro apresenta a função de risco acumulado \(\Lambda(t)\) estimada conforme a Equação 2.5. O segundo mostra a curva de sobrevivência de Nelson-Aalen através das relações entre as funções de análise de sobrevivência.
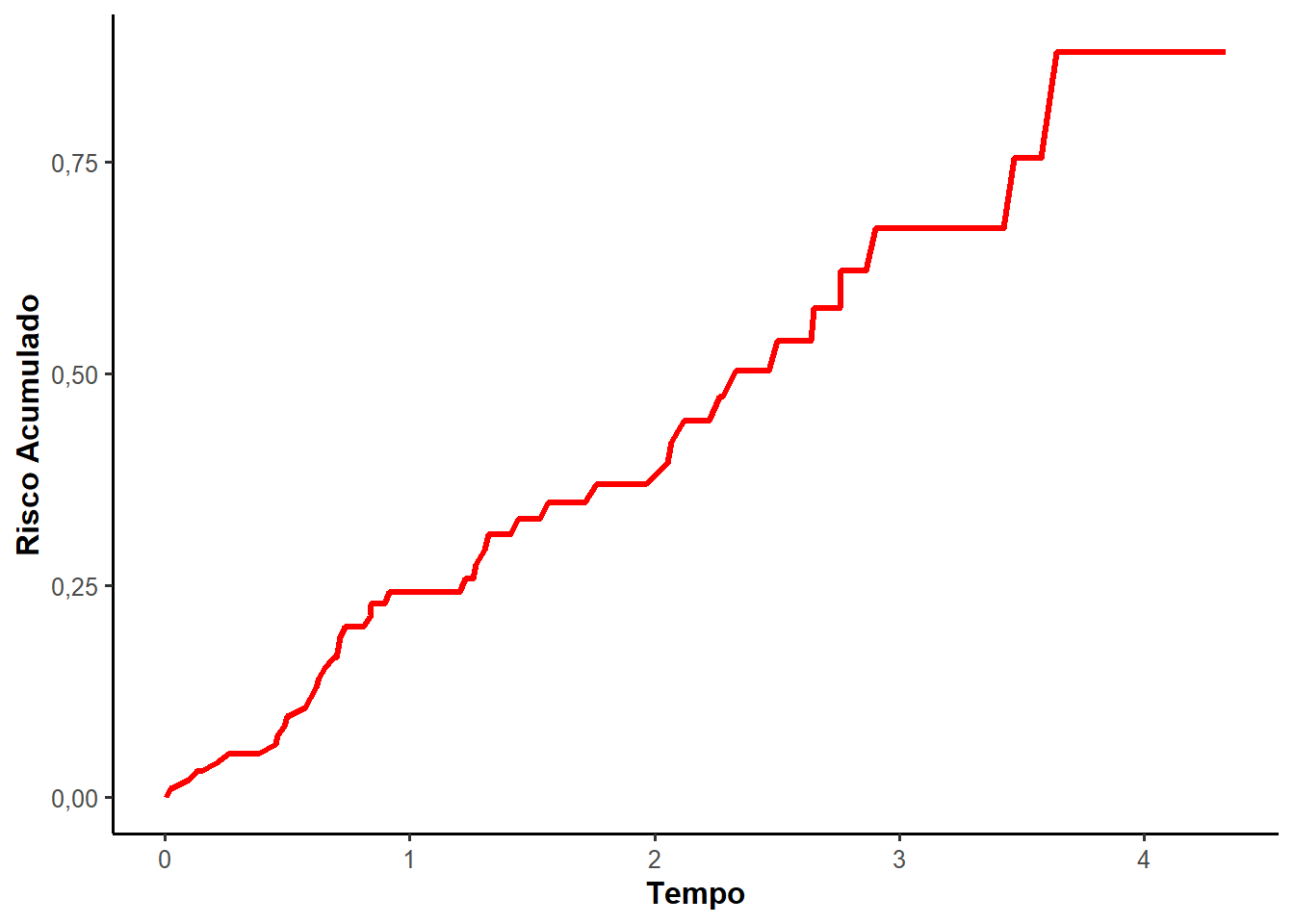
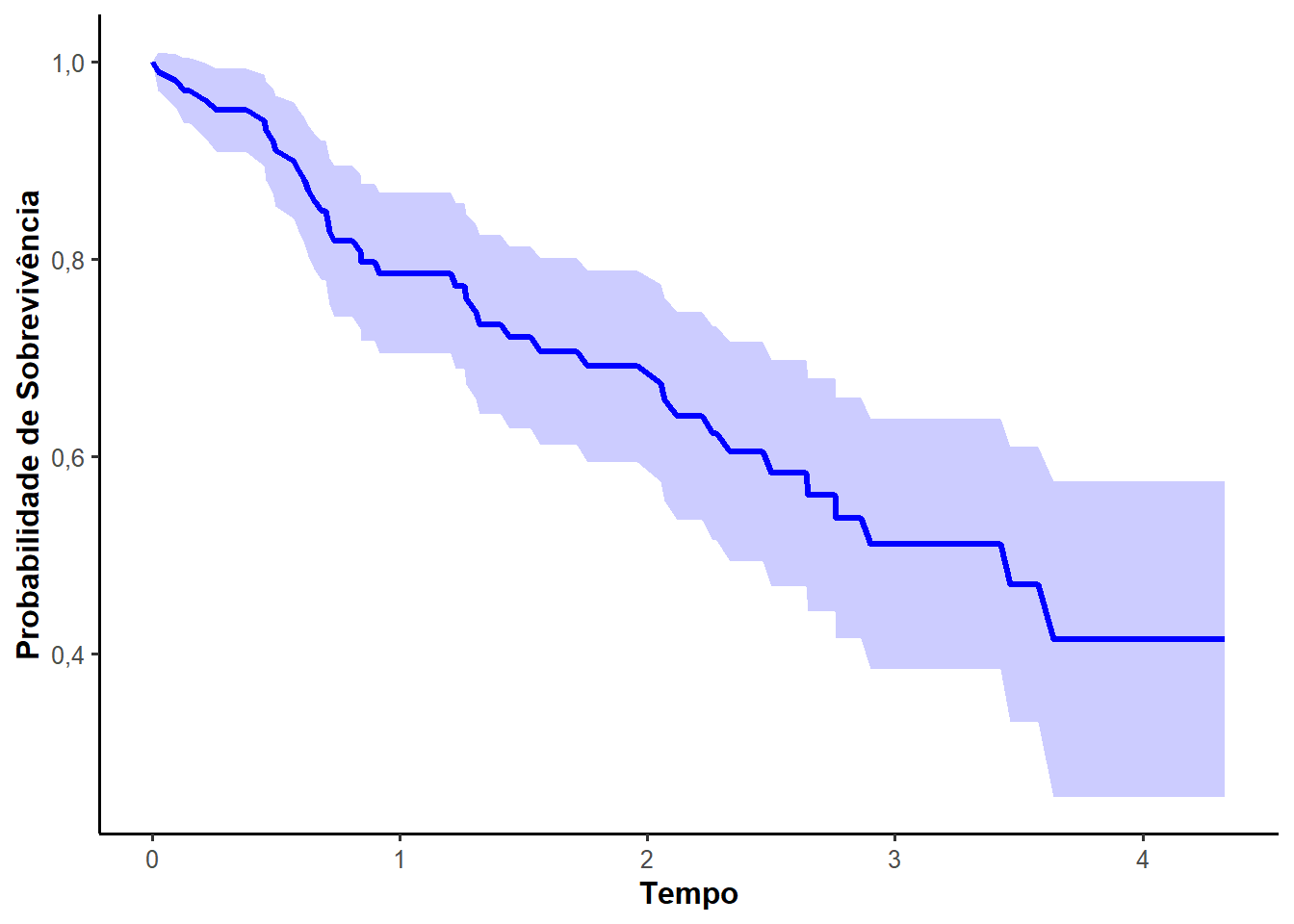
Vale destacar que o estimador de Nelson-Aalen apresenta, na maioria dos casos, estimativas próximas ao estimador de Kaplan-Meier. Bohoris (1994) mostrou que \(\hat{S}_{NA}(t) \geq \hat{S}_{KM}(t)\) para todo \(t\), isto é, as estimativas obtidas pelo estimador de Nelson-Aalen são maiores ou iguais às estimativas obtidas pelo estimador de Kaplan-Meier.
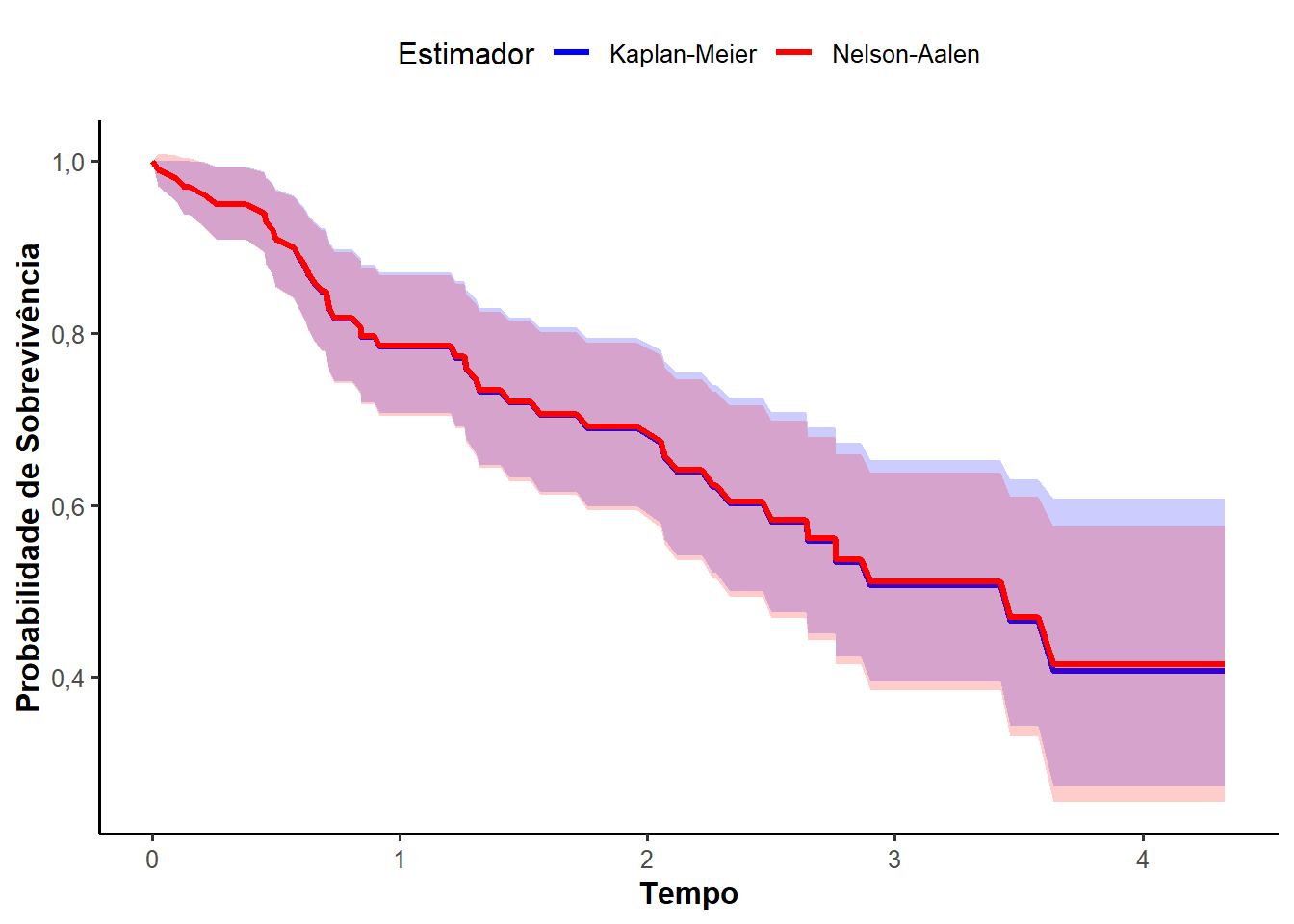
Considere um problema na área da saúde em que se deseja comparar dois grupos: um que receberá tratamento com uma determinada droga e outro que será o grupo controle. Estatísticas amplamente utilizadas para esse fim podem ser vistas como generalizações, para dados censurados, de testes não paramétricos bem conhecidos. Entre esses, o teste logrank (Mantel 1966) é o mais empregado em análises de sobrevivência. Gehan (1965) propôs uma generalização para a estatística de Wilcoxon. Outras generalizações foram introduzidas por autores como Peto e Peto (1972) e Prentice (1978), enquanto Latta (1981) utilizou simulações de Monte Carlo para comparar diversos testes não-paramétricos.
Nesta seção, será dada ênfase ao teste logrank, amplamente utilizado em análises de sobrevivência e particularmente adequado quando a razão entre as funções de risco dos grupos a serem comparados é aproximadamente constante. Ou seja, quando as populações apresentam a propriedade de riscos proporcionais.
A estatística do teste logrank baseia-se na diferença entre o número observado de falhas em cada grupo e o número esperado de falhas sob a hipótese nula. Essa abordagem é semelhante à do teste de Mantel e Haenszel (1959), que combina tabelas de contingência. Além disso, o teste logrank possui a mesma expressão do teste de escore para o modelo de regressão de Cox.
Considere, inicialmente, o teste de igualdade entre duas funções de sobrevivência \(S_{1}(t)\) e \(S_{2}(t)\). Seja \(t_{1} < t_{2} < \ldots < t_{k}\) a sequência dos tempos de falha distintos observados na amostra combinada, formada pela união das duas amostras individuais. Suponha que, no tempo \(t_{j}\), ocorram \(d_{j}\) falhas e que \(n_{j}\) indivíduos estejam sob risco imediatamente antes de \(t_{j}\) na amostra combinada. Nas amostras individuais, as quantidades correspondentes são \(d_{ij}\) e \(n_{ij}\), onde \(i = 1, 2\) representa o grupo e \(j = 1, \cdots, k\) indica o tempo de falha.
No tempo \(t_{j}\), os dados podem ser organizados em uma tabela de contingência \(2 \times 2\), onde \(d_{ij}\) representa o número de falhas e \(n_{ij} - d_{ij}\) o número de sobreviventes em cada grupo \(i\). Essa disposição está ilustrada na Tabela 2.1.
| Grupo 1 | Grupo 2 | ||
|---|---|---|---|
| Falha | \(d_{1j}\) | \(d_{2j}\) | \(d_{j}\) |
| Não Falha | \(n_{1j} - d_{1j}\) | \(n_{2j} - d_{2j}\) | \(n_{j} - d_{j}\) |
| \(n_{1j}\) | \(n_{2j}\) | \(n_{j}\) |
Condicionado à ocorrência de falhas e censuras até o tempo \(t_{j}\) (fixando as marginais das colunas) e ao número total de falhas no tempo \(t_{j}\) (fixando as marginais das linhas), a distribuição de \(d_{2j}\) é, então, uma hipergeométrica:
\[ \dfrac{ \binom{ n_{1j} }{ d_{1j} } \binom{ n_{2j} }{ d_{2j} } }{ \binom{ n_{j} }{ d_{j} } }. \]
A média de \(d_{2j}\) é dada por \(w_{2j} = n_{2j} d_{j} n_{j}^{-1}\). Isso significa que, na ausência de diferenças entre as duas populações no tempo \(t_{j}\), o número total de falhas (\(d_{j}\)) pode ser alocado entre as duas amostras proporcionalmente à razão entre o número de indivíduos sob risco em cada amostra e o número total sob risco.
A variância de \(d_{2j}\) obtida a partir da distribuição hipergeométrica é:
\[ (V_{j})_{2} = n_{2j}(n_{j} - n_{2j})d_{j}(n_{j} - d_{j}) n_{j}^{-2} (n_{j} - 1)^{-1}. \]
Portanto, a estatística \(d_{2j} - w_{2j}\) possui média zero e variância \((V_{j})_{2}\). Se as \(k\) tabelas de contingência forem independentes, um teste aproximado para avaliar a igualdade entre as duas funções de sobrevivência pode ser construído com base na seguinte estatística:
\[ T = \dfrac{ \left[ \sum_{j = 1}^{k} (d_{2j} - w_{2j}) \right]^{2} }{ \sum_{j = 1}^{k} (V_{j})_{2} }, \tag{2.7}\]
que, sob a hipótese nula \(H_{0}: S_{1}(t) = S_{2}(t)\) para todo \(t\) no período de acompanhamento, segue aproximadamente uma distribuição qui-quadrado com \(1\) grau de liberdade para amostras grandes.
Para exemplificar a aplicação do teste de logrank em dados reais, utilizou-se o conjunto de dados sobre Leucemia Pediátrica, disponível no Apêndice (A) do livro Análise de Sobrevivência Aplicada de Colosimo e Giolo (2006). Esses mesmos dados foram usados para gerar a Figura 2.1. O objetivo do teste realizado foi avaliar se as curvas de sobrevivência das categorias da covariável r6 são iguais, com as seguintes hipóteses:
\[ \begin{cases} H_{0}: \text{As curvas de sobrevivência dos grupos são iguais ao longo do tempo} \\ H_{1}: \text{As curvas de sobrevivência dos grupos são diferentes ao longo do tempo.} \end{cases} \]
Veja a saída resultante do teste realizado no software R:
# --------------------------------------------------------
# [2] TESTE DE LOG-RANK (Igual de Curvas de Sobrevivência)
# --------------------------------------------------------
# Ajustando a coluna r_6
dados.adj <- dados %>%
mutate(grupo = ifelse(r6 == 0, "Category Zero", "Category One"))
# Cria um objeto de Surv
dados.adj_surv <- Surv(dados.adj$tempos, dados.adj$cens)
# Aplica o Teste Logrank
logrank.test <- survdiff(dados.adj_surv ~ grupo, data = dados.adj)Ao fixar o nível de significância em 5% (\(\alpha = 0,05\)), rejeitamsos a hipótese nula. Essa conclusão baseia-se no valor \(p\) (probabilidade de significância) do teste sendo, \(p-valor \approx\) 0,0166. Como o \(p-valor < \alpha\), rejeita-se \(H_{0}\). Assim, conclui-se que as curvas de sobrevivência dos grupos são diferentes ao longo do tempo, ao nível de significância de 5%.
A generalização do teste logrank para a comparação de \(r > 2\) funções de sobrevivência, \(S_{1}(t), S_{2}(t), \ldots, S_{r}(t)\), é direta. Utilizando a mesma notação anterior, o índice \(i\) varia agora de \(1\) a \(r\). Assim, os dados podem ser organizados em uma tabela de contingência \(2 \times r\), onde cada coluna \(i\) contém \(d_{ij}\) falhas e \(n_{ij} - d_{ij}\) sobreviventes. Dessa forma, a Tabela 2.1 seria estendida para ter \(r\) colunas em vez de apenas duas.
Condicionada à experiência de falha e censura até o tempo \(t_{j}\) e ao número total de falhas no tempo \(t_{j}\), a distribuição conjunta de \(d_{2j}, \ldots,d_{rj}\) segue uma hipergeométrica multivariada, dada por:
\[ \dfrac{ \prod_{i = 1}^{r} \binom{ n_{ij }}{ d_{ij} } }{ \binom{ n_{j }}{ d_{j} } }. \]
A média de \(d_{ij}\) é \(w_{ij} = n_{ij} d_{j} n_{j}^{-1}\), bem como a variância de \(d_{ij}\) e a covariância de \(d_{ij}\) e \(d_{lj}\) são, respectivamente,
\[ (V_{j})_{ii} = n_{ij} (n_{j} - n_{ij}) d_{j} (n_{j} - d_{j}) n_{j}^{-2} (n_{j} - 1)^{-1} \]
e
\[ (V_{j})_{il} = - n_{ij} n_{lj} d_{j} (n_{j} - d_{j}) n_{j}^{-2} (n_{j} - 1)^{-1}. \]
A estatística \(v'_{j} = (d_{2j} - w_{2j}, \ldots, d_{rj} - w_{rj})\) possui média zero e matriz de variância-covariância \(V_{j}\), com dimensão \(r - 1\). A matriz \(V_{j}\) contém os termos \((V_{j}){ii}\) na diagonal principal e \((V_{j})_{il}\), \(i,l = 2, \ldots,r\), fora da diagonal principal.
A estatística \(v\), que agrega as contribuições de todos os tempos distintos de falha, é definida como:
\[ v = \sum_{j = 1}^{k} v_{j}, \]
onde \(v\) é um vetor de dimensão \((r - 1) \times 1\), cujos elementos correspondem às diferenças entre os totais observados e esperados de falhas.
Considerando, novamente, a independência das \(k\) tabelas de contingência, a variância de \(v\) é dada por \(V = V_{1} + \ldots + V_{k}\). Um teste aproximado para a igualdade das \(r\) funções de sobrevivência pode ser baseado na estatística:
\[ T = v´V^{-1} v, \tag{2.8}\]
que, sob a hipótese nula \(H_{0}\) (igualdade das curvas de sobrevivência), segue uma distribuição qui-quadrado com \(r - 1\) graus de liberdade para amostras grandes. Os graus de liberdade são \(r - 1\) em vez de \(r\), pois os elementos de \(v\) somam zero.
Uma aplicação para a comparação de \(r\) curvas de sobrevivência…
cat("Código em R a ser preenchido")Código em R a ser preenchido[…]